Аппаратное умножение BCD-чисел
Аппаратное умножение BCD-чисел на двух сумматорах и сдвиговом регистре.
Выношу из комментариев мою разработку — которая, надеюсь, поможет сделать хороший bcd-ускоритель для «ПМК мечты». Публикуется под GNU GPL v3. Перевод в «железо» данного алгоритма — серьёзная работа. Чтобы такой труд не был напрасным, я смоделировал алгоритм на Free Oberon.
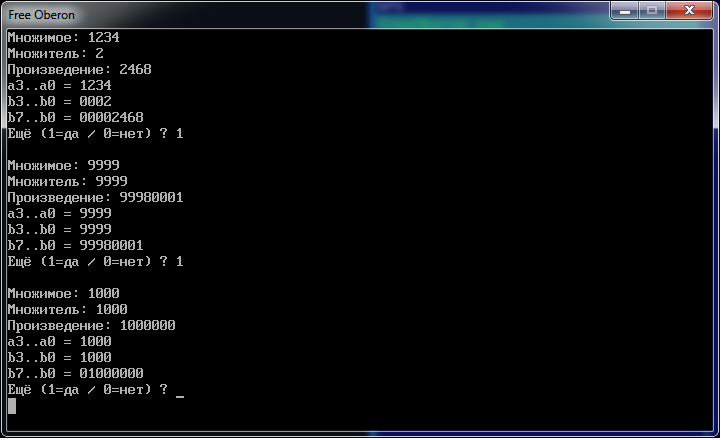
1. Полный алгоритм умножения двух bcd-чисел показывает, как использовать сдвиговый регистр b и один из сумматоров:
** Нужно три bcd-регистра **
Один 4-разрядный (CPU W/O):
a3..a0 Множимое, полноразрядный вход умножителя (половина адреса ПЗУ)
Один 5-разрядный (внутренний, без доступа из CPU):
s4..s0 Регистр на выходе умножителя, перед вторым входом сумматора
Один сдвиговый 9-разрядный объединяет два регистра (5+4):
b8..b4 Накопитель, регистр на выходе сумматора и перед первым его входом
b3..b0 Множитель, разряд b0 подаётся на второй вход умножителя
Также сюда засовываются слева разряды ответа
Доступ CPU к 9-разрядному регистру b:
b8 внутренний разряд, без доступа из CPU
b7..b4 CPU R/O старшие разряды ответа
b3..b0 CPU R/W множитель, а также младшие разряды ответа
** Иллюстрация **
a3 a2 a1 a0
b3 b2 b1 b0
————————————————
b0×a3 a2 a1 a0
b1×a3 a2 a1 a0
b2×a3 a2 a1 a0
b3×a3 a2 a1 a0
———————————————————————
d7 d6 d5 d4 d3 d2 d1 d0
** Алгоритм **
Загрузить a3..a0 множимым
Загрузить b3..b0 множителем
b8..b4 := 0 ; Можно сразу перенести s4..s0, без сложения
s4..s0 := a3..a0×b0 ; Умножитель, см. ниже пункт 2
b8..b4 += s4..s0 ; Для сумматора «в железе» много готовых решений
Сдвинуть b8..b0 вправо на 1 разряд ; Цифра d0 сейчас в b3
s4..s0 := a3..a0×b0
b8..b4 += s4..s0
Сдвинуть b8..b0 вправо на 1 разряд ; Цифры d1 d0 сейчас в b3 b2
s4..s0 := a3..a0×b0
b8..b4 += s4..s0
Сдвинуть b8..b0 вправо на 1 разряд ; Цифры d2 d1 d0 сейчас в b3 b2 b1
s4..s0 := a3..a0×b0
b8..b4 += s4..s0 ; Цифры d7..d3 сейчас в b8..b4
Сдвинуть b8..b0 вправо на 1 разряд ; Теперь ответ в b7..b0
Последний сдвиг можно не делать, если это упростит схему. b0 подаётся на вход умножителя, делать обвязку для считывания b0 процессором не обязательно. В этом случае ответ считывается из b8..b1.
Обратите внимание, что при сдвиге вправо в b8 записывается ноль. А раз там перед сложением всегда ноль, туда просто копируется тетрада из s4 — с учётом возможного переноса. Это упрощённый сумматор Σ'' из пункта 2.
2. Алгоритм выше четыре раза запускает следующий элементарный «умножитель», накапливая его результаты в сдвиговом регистре. Этот умножитель — самое главное в предложенной схеме. Для него и пригодится второй сумматор.
s4..s0 := a3..a0 × b0
Как реализовать этот умножитель? Делаются два ряда одинаковых ПЗУ на 100 разрядов каждое с таблицей умножения: младшая цифра ROM [a,b0] и старшая цифра ROMσ [a,b0]. Например ROM [9,9] = 1, а ROMσ [9,9]=8 в полном соответствии 9×9=81. (Вместо честных ПЗУ можно наколдовать восемь логических функций от 8 бит, не суть важно.) Считанные из ROM и ROMσ числа суммируются с перекосом на 1 разряд:
L3 L2 L1 L0 = тетрады, считанные из ROM[a3..a0,b0]
H3 H2 H1 H0 = тетрады, считанные из ROMσ[a3..a0,b0]
———————————————
s4 s3 s2 s1 s0
Сложение производит обычный многоразрядный сумматор. Ставятся в ряд четыре десятичных сумматора — первый Σ' из которых полусумматор, а последний Σ'' добавляет возможный перенос к старшей тетраде из ROMσ. Можно обойтись всего одним сумматором, протаскивая через него всё за четыре такта или наоборот, реализовать схему быстрого переноса (англ.), сложив всё за один такт.
s0 := ROM[a0,b0]
s1, σ1 := Σ'(ROM[a1,b0], ROMσ [a0,b0])
s2, σ2 := Σ (ROM[a2,b0], ROMσ [a1,b0], σ1)
s3, σ3 := Σ (ROM[a3,b0], ROMσ [a2,b0], σ2)
s4 := Σ'' (ROMσ [a3,b0], σ3)
Даже если реализовать в матрице только данное умножение на цифру, а не полную схему (1), этот элементарный «умножитель» существенно ускорит умножение процессором bcd-чисел. Конечно же, в рабочем варианте должно быть умножение 12-разрядных чисел минимум, а лучше 15-разрядных. Полную схему (1) можно реализовать программно-аппаратно. Добавив в матрицу сдвиговый регистр с ещё одним сумматором и продумав способ не гонять промежуточные результаты в процессор и обратно.
Последнее замечание к реализации. Множимое a3..a0 используется только для адресации ПЗУ. Его можно хранить отдельно от основной схемы, которая поставляет вторую половину адреса b0 для точного выбора нужных ячеек ПЗУ.
3. Моделирование на Обероне. К слову, за десятилетия моего опыта программирования и преподавания его же я не встречал более глючной среды разработки, чем Free Oberon. Это всего лишь версия 0.1.0 и надеюсь, к релизу все проблемы этого IDE исправят. К счастью, мне удалось разработать обходные манёвры вокруг каждого из глюков среды. Если что-то в моём псевдокоде непонятно, формальная нотация Оберона должна исправить любое недоразумение.
MODULE MulBCD; (* Моделирование аппаратного умножения bcd-чисел *)
IMPORT In, Out;
VAR
ia,ib,ic: INTEGER;
a: ARRAY 4 OF INTEGER; (* множимое *)
s: ARRAY 5 OF INTEGER; (* произведение, внутренний регистр *)
b: ARRAY 9 OF INTEGER; (* b8..b4 накопитель, b3..b0 множитель, b8..b0 ответ *)
PROCEDURE StoreBCD(x: INTEGER; VAR a: ARRAY OF INTEGER; n: INTEGER);
VAR i: INTEGER;
BEGIN (* Записать число x в n младших разрядов bcd-числа a *)
i:=0;
WHILE i<n DO a[i]:=x MOD 10; x:=x DIV 10; INC(i) END
END StoreBCD;
PROCEDURE PrintBCD(VAR a: ARRAY OF INTEGER; n: INTEGER);
BEGIN (* Вывести n младших разрядов bcd-числа a *)
REPEAT DEC(n); Out.Char(CHR(48+a[n])) UNTIL n<=0;
Out.Ln
END PrintBCD;
PROCEDURE ClearBCD(VAR a: ARRAY OF INTEGER; l,r: INTEGER);
BEGIN REPEAT a[r]:=0; INC(r) UNTIL r>l
END ClearBCD; (* Обнулить разряды l..r bcd-числа a *)
PROCEDURE Multiply; (* s4..s0 := a3..a0*b0 *)
VAR
o1, o2, o3: BOOLEAN; (* Переносы между тетрадами *)
PROCEDURE ROM(i,j: INTEGER): INTEGER;
BEGIN RETURN (i*j) MOD 10 (* Таблица умножения, младшая цифра *)
END ROM;
PROCEDURE ROMo(i,j: INTEGER): INTEGER;
BEGIN RETURN (i*j) DIV 10 (* Таблица умножения, старшая цифра *)
END ROMo;
PROCEDURE Sum0(VAR c: INTEGER; VAR f: BOOLEAN; i,j: INTEGER);
BEGIN (* Полусумматор, c:=i+j и флаг переноса f *)
c := (i+j) MOD 10;
f := (i+j) > 9
END Sum0;
PROCEDURE Sum(VAR c: INTEGER; VAR f1: BOOLEAN; i,j: INTEGER; f0: BOOLEAN);
BEGIN (* Сумматор, c:=i+j+f0 и флаг переноса f1 *)
IF f0 THEN c:=i+j+1 ELSE c:=i+j END;
f1 := c > 9;
c := c MOD 10
END Sum;
PROCEDURE SumL(i: INTEGER; f: BOOLEAN): INTEGER;
BEGIN IF f THEN RETURN i+1 ELSE RETURN i END
END SumL; (* Завершающий сумматор, увеличить i если перенос f *)
BEGIN (* Главное, что надо реализовать в железе *)
s[0] := ROM(a[0],b[0]);
Sum0(s[1],o1, ROM(a[1],b[0]),ROMo(a[0],b[0]));
Sum(s[2],o2, ROM(a[2],b[0]),ROMo(a[1],b[0]),o1);
Sum(s[3],o3, ROM(a[3],b[0]),ROMo(a[2],b[0]),o2);
s[4] := SumL(ROMo(a[3],b[0]),o3)
END Multiply;
PROCEDURE Add; (* b8..b4 += s4..s0 *)
VAR i,x,c: INTEGER;
BEGIN (* Обычный bcd-сумматор *)
i:=0; c:=0;
REPEAT
x := b[4+i]+s[i]+c;
b[4+i] := x MOD 10;
c := x DIV 10;
INC(i)
UNTIL i>4
END Add;
PROCEDURE Shift; (* Сдвинуть b8..b0 вправо на 1 разряд *)
VAR i: INTEGER;
BEGIN (* Обычный логический bcd-сдвиг вправо *)
i:=0;
WHILE i<8 DO b[i]:=b[i+1]; INC(i) END;
b[8]:=0
END Shift;
BEGIN
REPEAT
Out.String('Множимое: '); In.Int(ia);
Out.String('Множитель: '); In.Int(ib);
Out.String('Произведение: '); Out.Int(ia*ib,0); Out.Ln;
StoreBCD(ia,a,4); Out.String('a3..a0 = '); PrintBCD(a,4);
StoreBCD(ib,b,4); Out.String('b3..b0 = '); PrintBCD(b,4);
ClearBCD(b,8,4);
Multiply; Add; Shift; (* Цифра d0 сейчас в b3 *)
Multiply; Add; Shift; (* Цифры d1 d0 сейчас в b3 b2 *)
Multiply; Add; Shift; (* Цифры d2 d1 d0 сейчас в b3 b2 b1 *)
Multiply; Add; Shift; (* Теперь ответ в b7..b0 *)
Out.String('b7..b0 = '); PrintBCD(b,8);
Out.String('Ещё (1=да / 0=нет) ? '); In.Int(ic); Out.Ln
UNTIL ic=0
END MulBCD.
История:
- 17 сентября 2017. «Причесал» схему суммирования в умножителе. Привёл модель в соответствие с новой схемой.
- 15 сентября 2017. Первая публикация алгоритма. Сдвиговый регистр двойного размера поставляет умножителю младшие разряды второго множителя и сохраняет младшие разряды ответа.
